机器学习课程笔记

机器学习笔记

初始机器学习

人工智能概念

• 是研究那些使理解、推理和行为成为可能的计算

• 是一种能够执行需要人类智能的创造性机器的技术

• 是智能机器所执行的通常与人类智能有关联的智能行为，如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习、问题求解等思维活动

人工智能要素

• 知识 - 人工智能之源: 知识表示 → 知识推理 → 行业应用
• 数据 - 人工智能之基: 数据 → 信息 → 知识
• 算法 - 人工智能之魂: 实现上述流程的策略机制

机器学习概念

对于机器学习的两种定义：

• “the field of study that gives computers the ability to learn without being explicitly programmed.” - Arthur Samuel

  “使计算机能够在没有明确编程的情况下获得学习能力的研究领域。”

• “A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.” - Tom Mitchell

  “一个计算机程序可以从经验 E 中学习关于某类任务 T 的知识，并通过性能度量 P 来衡量。如果它在任务 T 上的性能（通过 P 衡量）随着经验 E 的增加而提高，那么就说该程序从经验 E 中学习。”

基本术语：

• 样本
• 数据集：样本集合。训练集、测试集
• 特征（属性）：Humid，{一组样本的某一个属性值}
• 标签：EnjoySpt，结果，样本的定性
• 预测模型：函数 f(样本) = 预测标签值
• 学习
• 训练：通过历史数据获取预测模型函数
• 预测
• 泛化能力：模型对新样本的预测能力
• 有监督：样本标签参与训练模型的学习任务
• 无监督：无需标签参与的学习任务
• 假设空间：Hypothesis space
  • 数据集属性的取值限制了假设空间的表达
  • 表达符号：
    • “*”：属性对假设成立与否没有限制

      • 例如：

      • 等价于：只要根蒂蜷缩且敲声浊响，无论什么色泽都是好瓜

    • “∅”：假设不可能成立
      • 例如：若世界上根本不存在好瓜这种东西，则用∅表示该假设

任何机器学习问题可以归于两大类之一：监督学习（Supervised Learning），或无监督学习（Unsupervised Learning，或称非监督学习）。当然，还有半监督学习、强化学习等，尚不在讨论范围内。

监督学习

监督学习使用有标签的数据集，其任务是学习一个模型，使模型能够对任意给定的输入，对其相应的输出做出一个好的预测。

监督学习问题被分为回归（Regression）和分类（Classification）问题：

• 回归问题：将输入变量映射到某个连续函数，即预测一个连续值；
• 分类问题：将输入变量映射到离散的类别中，即预测一个离散值。

有监督学习任务特点

• 训练集有标签
• 对训练集表示的假设进行搜索
• 搜索过程直接获得标签的监督反馈

无监督学习

在无监督学习中，使用的数据集没有标签，不知道结果会是什么样子，但可以通过聚类的方式从数据中提取一个特殊的结构。

• 聚类
• 降维

无监督学习任务特点

• 可以无训练过程
• 直接对数据进行基于特征值的建模
• 寻找数据中的隐藏结构

模型评估

误差

• 训练误差：在训练集上的误差
  • 误差太小 -> 过拟合(overfitting) -> 泛化能力弱
  • 误差太大 -> 欠拟合(underfitting)
• 泛化误差：在“未来”样本上的误差
  • 误差越小 -> 泛化能力越强
• 测试误差：在测试集上的误差
  • 从已有数据中划分出测试集用于近似泛化误差

模型参数调整

1. 将数据集分为训练集、验证集和测试集。
2. 使用训练集训练模型。
3. 使用验证集选择模型参数。
4. 使用训练集 + 验证集重新训练模型 (使用最佳参数)。
5. 使用测试集进行最终性能度量。

参数类型

• 算法参数 (超参数): 人工设定，在学习开始前定义。
• 模型参数: 由学习过程确定。
• 所有参数都会影响模型性能。

模型评估的三个关键问题:

1. 评估方法: 如何获取测试结果？

   • 留出法 (Hold-out)：将数据集划分为训练集和测试集，多次重复划分以减小误差。注意保持数据分布一致性，测试集大小适中 (e.g., 20%-30%)。
   • 交叉验证法 (Cross Validation)：将数据集等分为 k 份，轮流将每一份作为测试集，其余作为训练集，取平均误差作为评估结果。k 常取 10。
   • 自助法 (Bootstrap)：适用于小样本数据集。通过有放回采样生成训练集，未被采样的数据作为测试集。注意：采样会改变数据分布，可能影响评估结果。

2. 性能度量 如何评估性能优劣？

   • 均方误差 (MSE)：回归任务常用。
   • 错误率和精度：分类任务常用。
   • 查准率 (Precision)：预测为正的样本中有多少是真正的正例。
   • 查全率 (Recall)：真正的正例中有多少被预测为正例。
   • ROC 曲线和 AUC 值：用于评估分类器在不同阈值下的性能。AUC 值越大，性能越好。

3. 比较检验 如何判断哪种算法更好？

   • 为什么不直接比较测试集上的性能？ 因为测试集性能 ≠ 泛化性能，且测试集性能对测试集本身很敏感，存在随机性。

   • 统计假设检验：用于判断模型性能差异的显著性。

     • 单个模型：对多次测试的错误率求均值、方差（t 检验）

     • 两模型比较：交叉验证 t 检验、k 折交叉验证、McNemar 检验、Wilcoxon 符号秩检验。
     • 多模型比较：Friedman 检验 + Nemenyi 后续检验、Bonferroni-Dunn 检验。

   • 假设检验 (单个模型): 对学习器泛化错误率的猜想进行检验，评估其置信度。

机器学习开发流程

---

机器学习模型

K近邻算法

K近邻算法（K-Nearest Neighbors, KNN）是一种简单但有效的监督学习算法，可用于分类和回归任务。它的核心思想是：如果一个样本在特征空间中的 k 个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

应用场景：文本分类、图像识别、推荐系统、异常检测…

• 算法流程：

  1. 计算距离： 计算待分类样本与训练集中每个样本之间的距离。常用的距离度量方法有欧氏距离、曼哈顿距离、汉明距离等。
     • 欧式距离：直线距离
     • 曼哈顿距离：也称为城市街区距离，计算的是两个点在坐标轴上绝对差值的累加
     • 汉明距离：计算两个等长字符串之间的差异，表示两个字符串中对应位置的字符不同的数量。Exp. ‘110011’和‘111111’的汉明距离为2
  2. 寻找最近邻：选择距离待分类样本最近的k个样本。
  3. 计算k个邻居的投票权重
  4. 投票决定： 对于分类任务，k个最近邻中哪个类别的样本最多，就将待分类样本归为哪一类。对于回归任务，则将k个最近邻样本的输出值的平均值作为待分类样本的预测值。

  算法特点：

  • 简单易懂，易于实现。影响因素：K值、相似性度量、投票策略
  • 无需训练： KNN是一种“懒惰学习（lazy learn）”算法，它并不需要显式的训练过程，而是直接将训练数据存储起来，在需要分类新样本时才进行计算。
  • 对异常值敏感： 由于KNN依赖于距离度量，因此它对异常值比较敏感。
  • 计算复杂度高： 当训练集很大时，计算待分类样本与所有训练样本之间的距离会非常耗时。
  • k值的选择很重要： k值太小，模型容易过拟合、被噪点干扰；k值太大，模型容易欠拟合、不相似的邻居参与决策、分类性能弱。k值通常需要通过交叉验证等方法来选择。
  • 特征缩放很重要： 由于KNN依赖于距离度量，因此不同特征的取值范围差异较大时，需要进行特征缩放，例如归一化或标准化。

线性模型

分类与回归

• 工作流程：输入—>模型—>输出
• 应用：物体识别、超像素、降维…

一、 线性模型概览

• 作用: 用一条直线 (或超平面) 来预测或分类数据。
• 公式: f(x) = w1x1 + w2x2 + ... + wdxd + b (简单来说就是 y = wx + b 的扩展版)
• 关键: 找到合适的 w (权重) 和 b (偏置)。
• 应用: 回归 (预测连续值，如房价) 和分类 (预测类别，如好/坏瓜)。

二、 线性回归 (预测连续值)

• 目标: 找到一条直线，让所有数据点尽可能靠近这条直线。
• 方法: 最小二乘法 (让预测值和真实值之间的差距总和最小)。

三、 逻辑回归 (二分类)

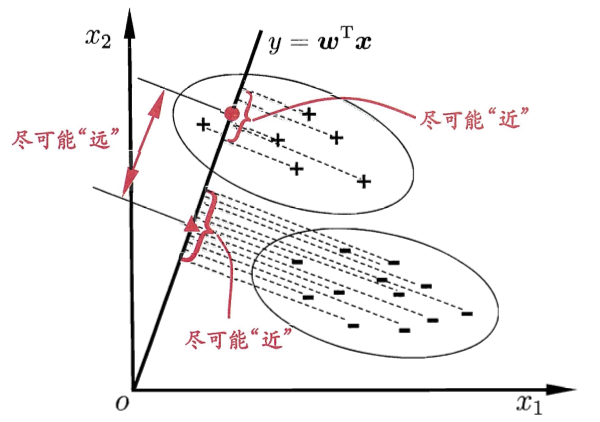
• 目标: 找到一条直线，把两类数据分开。 \(使 z = \mathbf{w}^T\mathbf{x} + b 的值对应于样本的两个类别:0, 1\)

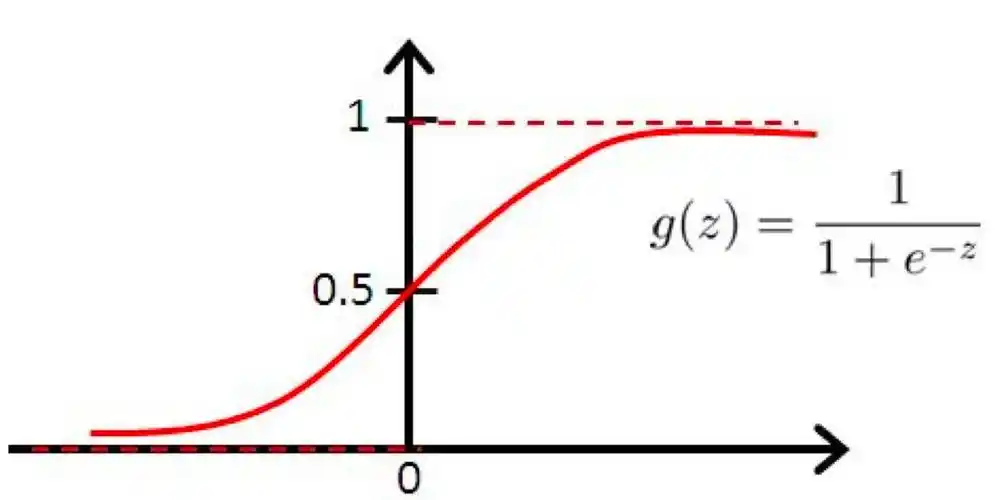
• 方法: 用 Sigmoid 函数把直线算出的值“压缩”到 0 和 1 之间，表示属于某一类的概率。

  

• 名字叫“回归”，但实际上是用来做分类的。

四、 线性判别分析 (LDA)

• 目标: 把数据投影到一条直线上，让同一类的数据点挨得近，不同类的数据点离得远。

  

• 作用: 有监督的降维技术，可以简化数据。

五、 多分类

• 思路: 把多分类问题变成多个二分类问题。
• 常用方法:
  • 一对一 (One vs. One): 每两个类别都训练一个分类器。（ N(N-1)/2 个分类器）
  • 一对其余 (One vs. Rest): 每个类别都跟其他所有类别训练一个分类器。（N个分类器）
  • 多对多 (Many vs. Many): 使用 ECOC 技术，让分类更有容错性。

总结:

线性模型是一种简单但强大的机器学习模型，可以用来做回归和分类。线性回归用来预测数值，逻辑回归用来做二分类，LDA 用来降维和分类，多分类问题可以通过一些策略转化为二分类问题。

决策树

好的，我将更详细地介绍决策树，并提供更充实的笔记。

决策树 (Decision Tree)

一、 概述

决策树是一种常用的监督学习算法，可用于分类和回归问题。它通过学习一系列 if-then-else 规则来逼近一个目标函数，从而预测目标变量的值。决策树模型具有树状结构，易于理解和解释，因此在实际应用中非常受欢迎。

二、 核心概念

1. 节点 (Node)
   • 根节点 (Root Node): 表示整个数据集，位于树的顶端。
   • 内部节点 (Internal Node): 表示一个特征或属性的测试。
   • 叶节点 (Leaf Node): 表示一个类别标签（分类问题）或一个数值（回归问题）。

2. 分支 (Branch)：表示一个属性测试的结果，连接父节点和子节点。

3. 划分 (Splitting)：根据某个属性的值将数据集分成多个子集的过程。

4. 决策规则 (Decision Rule)：从根节点到叶节点的路径上的一系列条件判断。

三、 构建决策树的步骤

构建决策树是一个递归的过程，主要步骤如下：

1. 特征选择： 从训练数据中选择一个最佳的特征作为当前节点的划分标准。
2. 决策树生成： 根据选定的特征，将数据集划分成多个子集，并对每个子集递归地调用步骤 1 和 2，直到满足停止条件。
3. 剪枝： 为了防止过拟合，需要对生成的决策树进行剪枝，去掉一些不必要的分支。

四、 特征选择

特征选择是构建决策树的关键步骤，目标是选择一个能够最好地区分不同类别的特征。常用的特征选择方法有：

1. 信息增益 (Information Gain) - ID3 算法使用

   • 熵 (Entropy): 度量数据集的纯度或不确定性。熵越大，数据集越混乱。公式如下：

     $Ent(D) = -\sum_{k=1}^{

     y

     } p_k \log_2 p_k$

     其中，$D$ 表示数据集，$

     y

     $ 表示类别数量，$p_k$ 表示第 $k$ 类样本占总样本数的比例。

   • 条件熵 (Conditional Entropy): 在已知某个特征的条件下，数据集的熵。

   • 信息增益： 表示在已知某个特征的条件下，数据集的不确定性减少的程度。信息增益越大，说明该特征的分类能力越强。公式如下：

     $Gain(D, a) = Ent(D) - \sum_{v=1}^{V} \frac{

     D^v

     }{

     D

     } Ent(D^v)$

     其中，$a$ 表示特征，$V$ 表示特征 $a$ 可能的取值数量，$D^v$ 表示特征 $a$ 取值为 $v$ 的样本子集。

   • 选择标准： 选择信息增益最大的特征作为划分特征。

2. 信息增益率 (Information Gain Ratio) - C4.5 算法使用

   • 动机： 信息增益倾向于选择取值较多的特征，为了解决这个问题，引入了信息增益率。

   • 公式：

     $Gain_ratio(D, a) = \frac{Gain(D, a)}{IV(a)}$

     其中，$IV(a) = -\sum_{v=1}^{V} \frac{

     D^v

     }{

     D

     } \log_2 \frac{

     D^v

     }{

     D

     }$ 称为特征 $a$ 的“固有值”(Intrinsic Value)。特征 $a$ 的可能取值越多，$IV(a)$ 的值通常越大。

   • 选择标准： 选择信息增益率最大的特征作为划分特征。

3. 基尼指数 (Gini Index) - CART 算法使用

   • 基尼值 (Gini Value): 反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。基尼值越小，数据集的纯度越高。公式如下：

     $Gini(D) = \sum_{k=1}^{

     y

     } \sum_{k’ \neq k} p_k p_{k’} = 1 - \sum_{k=1}^{

     y

     } p_k^2$

   • 基尼指数： 属性 $a$ 的基尼指数定义为：

     $Gini_index(D, a) = \sum_{v=1}^{V} \frac{

     D^v

     }{

     D

     } Gini(D^v)$

   • 选择标准： 选择基尼指数最小的特征作为划分特征。

五、 决策树生成算法

1. ID3 算法
   • 使用信息增益作为特征选择标准。
   • 步骤：
     1. 计算所有特征的信息增益。
     2. 选择信息增益最大的特征作为当前节点的划分特征。
     3. 根据该特征的不同取值，将数据集划分成多个子集。
     4. 对每个子集递归地调用步骤 1-3，直到满足停止条件（例如：所有样本属于同一类别，或没有可用特征）。
   • 缺点：
     • 偏向于选择取值较多的特征。
     • 不能处理连续值特征。
     • 不能处理缺失值。
     • 容易过拟合。

2. C4.5 算法

   • 使用信息增益率作为特征选择标准。
   • 可以处理连续值特征：采用二分法将连续值离散化。
   • 可以处理缺失值：将缺失值分配到所有子集中，权重根据子集中样本数量调整。
   • 步骤： 与 ID3 类似，但使用信息增益率代替信息增益。
   • 缺点： 仍然容易过拟合。

3. CART 算法 (Classification and Regression Tree)

   • 使用基尼指数作为特征选择标准。
   • 可以用于分类和回归问题。
   • 生成的是二叉树。
   • 步骤：
     1. 对每个特征的每个可能取值，将数据集分成两部分。
     2. 计算每个划分的基尼指数。
     3. 选择基尼指数最小的划分作为当前节点的划分。
     4. 对每个子集递归地调用步骤 1-3，直到满足停止条件。

六、 剪枝 (Pruning)

剪枝是防止决策树过拟合的重要手段，通过去掉一些分支来降低模型的复杂度，提高模型的泛化能力。剪枝方法主要有两种：

1. 预剪枝 (Pre-pruning): 在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能的提升，则停止划分并将当前节点标记为叶节点。
   • 方法： 例如，限制树的深度、限制叶节点的样本数量、设定信息增益/增益率/基尼指数的阈值等。
   • 优点： 降低过拟合风险，减少训练时间。
   • 缺点： 可能导致欠拟合。
2. 后剪枝 (Post-pruning): 先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化性能的提升，则将该子树替换为叶节点。
   • 方法： 例如，代价复杂度剪枝 (Cost-Complexity Pruning, CCP)。
   • 优点： 通常比预剪枝保留更多的分支，欠拟合风险小，泛化性能往往优于预剪枝。
   • 缺点： 训练时间开销大。

七、 连续值和缺失值处理

1. 连续值处理

   • 二分法 (Bi-partition): C4.5 算法采用的策略。将连续属性的取值排序，然后选择一个划分点，将数据集分成两部分。选择划分点的标准是信息增益最大化。

2. 缺失值处理

   • C4.5 算法的处理方法：
     • 如何选择划分属性？ 使用没有缺失值的样本子集计算信息增益率。
     • 给定划分属性，如何划分带有缺失值的样本？ 将缺失值样本以不同的概率划分到不同的子节点中，概率的大小根据其他非缺失属性该样本的比例来确定。

八、 决策树的优缺点

优点：

• 易于理解和解释，决策过程可视化。
• 需要很少的数据预处理，可以处理数值型和类别型数据。
• 可以处理多输出问题。
• 对缺失值不敏感。

缺点：

• 容易过拟合，需要进行剪枝。
• 可能不稳定，数据的小变化可能会导致生成完全不同的树。
• 决策树学习算法是基于启发式的，例如在每个节点进

支持向量机 SVM

一、 概述

支持向量机 (Support Vector Machine, SVM) 是一种经典的监督学习算法，主要用于解决二分类问题，也可扩展到多分类和回归问题。SVM 的核心思想是在特征空间中寻找一个最优的超平面，将不同类别的数据样本尽可能清晰地分开，同时最大化分类间隔。

二、 核心概念

1. 超平面 (Hyperplane)： 在 n 维特征空间中，超平面是一个 n-1 维的子空间，用于划分数据。在二维空间中，超平面是一条直线；在三维空间中，超平面是一个平面。超平面的数学表达式为：$w^Tx+b=0$，其中 𝑤 为法向量，𝑏为偏置项。
2. 间隔 (Margin)： 间隔是指两个不同类别中距离超平面最近的样本点到超平面的距离之和。这些最近的样本点被称为支持向量。
3. 支持向量 (Support Vectors)： 支持向量是训练数据集中距离超平面最近的那些样本点，它们位于间隔边界上，对确定最优超平面起着关键作用。
4. 目标： SVM 的目标是找到一个超平面，使得所有样本点都被正确分类，并且间隔最大化。

三、 线性可分支持向量机

当训练数据线性可分时，即存在一个超平面能够将所有样本点完全正确地划分到两侧，此时的 SVM 称为线性可分支持向量机。

1. 优化目标： 找到一个超平面，满足以下两个条件：
   • 所有样本点被正确分类。
   • 间隔最大化。
2. 关键因素： 最优超平面的确定仅依赖于支持向量，与其他样本点无关。

四、 线性支持向量机

当训练数据线性不可分时，即不存在一个超平面能够将所有样本点完全正确地划分，此时需要引入“软间隔”的概念，允许部分样本点不满足约束条件。

1. 软间隔 (Soft Margin)： 允许部分样本点不满足间隔大于等于 1 的约束，即允许一些样本点出现在间隔边界内部，甚至被错误分类。
2. 惩罚因子 (Penalty Parameter)： 为了平衡间隔最大化和错误分类样本数量，引入惩罚因子 C。C 值越大，对错误分类的惩罚越大，模型越倾向于将所有样本点正确分类；C 值越小，对错误分类的容忍度越高，模型越倾向于获得更大的间隔。
3. 优化目标： 在最大化间隔的同时，最小化错误分类样本点的数量。

五、 非线性支持向量机

当训练数据线性不可分，且无法通过简单的引入的软间隔来解决时，可以利用核函数将数据映射到高维特征空间，使得数据在高维空间中线性可分。

1. 核函数 (Kernel Function)： 核函数是一个函数，它接受两个样本点作为输入，返回它们在映射后的高维特征空间中的内积。核函数避免了直接计算高维空间中的映射，从而降低了计算复杂度。
2. 常用核函数：
   • 线性核 (Linear Kernel)： 不进行映射，直接在原始特征空间中计算内积。
   • 多项式核 (Polynomial Kernel)： 将数据映射到多项式特征空间。
   • 高斯核 (Gaussian Kernel) / 径向基函数核 (RBF Kernel)： 将数据映射到无限维特征空间，是最常用的核函数之一。

六、 序列最小优化算法 (Sequential Minimal Optimization, SMO)

SMO 算法是一种用于求解 SVM 优化问题的迭代算法。它将原始的二次规划问题分解成多个只包含两个变量的子问题，并通过迭代求解这些子问题来逼近原始问题的最优解。

七、 支持向量回归 (Support Vector Regression, SVR)

SVM 也可以用于回归问题，称为支持向量回归 (SVR)。SVR 的目标是找到一个函数，使得所有样本点到该函数的距离都小于一个预设的阈值，并且该函数的复杂度尽可能低。

八、 优缺点

优点：

• 高维空间有效性： 在高维特征空间中仍然表现出色。
• 样本效率： 在样本数量相对较少的情况下也能取得良好的效果。
• 内存效率： 仅需存储支持向量，内存占用相对较小。
• 非线性处理能力： 通过核技巧可以有效处理非线性问题。

缺点：

• 训练时间： 当样本数量非常大时，训练时间可能较长。
• 缺失值敏感： 对缺失数据较为敏感，需要进行预处理。
• 参数敏感性： 核函数的选择和参数的调节对模型性能影响较大，需要仔细调优。

贝叶斯分类器 (Bayesian Classifier)

贝叶斯决策论：概率知识+决策损失认知—>最优决策

• 贝叶斯决策论是统计学中进行决策的基本方法，它基于概率和损失来评估不同决策的优劣。在分类问题中，贝叶斯决策论的目标是最小化总体风险。

核心思想

• 选择能够最小化风险的类别。

• 风险评估： 将一个真实类别为 A 的样本误分类为 B，会产生一定的损失。基于后验概率（即已知样本特征的情况下，属于各个类别的概率），可以计算出将样本分类为不同类别所带来的风险。
• 贝叶斯最优分类器： 对于每个样本，选择能够使风险最小的类别进行分类，这样的分类器被称为贝叶斯最优分类器。

二、 如何获得后验概率？

后验概率是指在已知样本特征的情况下，样本属于各个类别的概率。获取后验概率是贝叶斯分类的关键。

• 理论方法： 进行大量的观察，以获得接近真实的后验概率。但在现实中往往不可行，因为这需要极大的数据量和计算资源。
• 现实途径： 基于有限的观察数据，尽可能准确地估计后验概率。

三、 估计后验概率的策略

主要有两种策略来估计后验概率：

1. 判别式模型 (Discriminative Models)： 直接对后验概率进行建模。例如，决策树和支持向量机 (SVM) 都属于判别式模型。它们直接学习一个分类边界或者函数，将不同类别区分开来。
2. 生成式模型 (Generative Models)： 先对数据的联合概率分布进行建模，然后利用贝叶斯定理间接得到后验概率。贝叶斯分类器就属于生成式模型。

四、 贝叶斯定理

贝叶斯定理是连接先验概率、似然度和后验概率的桥梁。

• 先验概率： 指的是样本空间中各类样本所占的比例。例如，一个班级中男生和女生的比例。通常可以通过统计样本出现的频率来估计。
• 似然度（条件概率）： 指的是在已知样本属于某个类别的前提下，样本具有当前特征的概率。例如，已知一个学生是男生，那么他身高 1.8 米的概率。这是在估计过程中遇到的主要难点。
• 证据因子： 与类别无关，对于所有类别都是相同的，因此在比较不同类别的后验概率时可以忽略。

五、 极大似然估计 (Maximum Likelihood Estimation, MLE)

极大似然估计是一种常用的估计似然度的方法。

• 基本思想： 假设样本的特征服从某种概率分布，这种概率分布由一些参数决定。然后，利用训练数据来估计这些参数。使得在该参数下，观测到当前训练数据的概率最大。
• 关键： 需要对数据的分布做出假设。如果假设的分布形式与真实分布相符，那么估计效果较好；否则，估计结果可能会产生较大偏差。
• 实际应用： 在工程应用中，往往需要对问题中的数据分布有一定的基础认知，才能选择合适的分布进行极大似然估计，否则容易产生误导性的结果。

六、 朴素贝叶斯分类器 (Naive Bayes Classifier)

朴素贝叶斯分类器是一种常用的贝叶斯分类器。

• 核心假设： 假设样本的所有特征在给定类别的情况下相互独立。这是一个较强的假设，但在实际应用中往往能够取得不错的效果。
• 分类过程：
  1. 根据训练数据估计每个类别的先验概率。
  2. 根据训练数据和特征独立性假设，估计每个特征在每个类别下的条件概率（似然度）。
  3. 对于待分类样本，根据贝叶斯定理计算其属于每个类别的后验概率。
  4. 将样本分类到后验概率最大的类别。
• 参数估计：
  • 先验概率： 通过训练数据中每个类别的样本占比来估计。
  • 条件概率：
    • 离散型特征： 统计训练数据中，每个类别下该特征取各个值的频率。
    • 连续型特征： 通常假设特征服从某种概率分布（如高斯分布），然后根据训练数据估计该分布的参数（如均值和方差）。

集成模型 (Ensemble Models)

核心思想： 集成模型通过结合多个弱学习器（基学习器）来构建一个强学习器，以提高模型的泛化能力和鲁棒性。

一、集成模型 vs. 非集成模型

类型	描述	迭代次数	训练方式
单一模型	使用单个学习器进行预测	1 次	-
Bagging	并行训练多个基学习器，每个基学习器在不同的自助采样数据集上训练	多次	并行
Boosting	顺序训练多个基学习器，每个基学习器都试图纠正前一个基学习器的错误	多次	串行

二、Bagging (Bootstrap Aggregating)

1. 自助采样 (Bootstrap Sampling)： 对给定的数据集进行 有放回采样，产生 $T$ 个训练集。
2. 训练基学习器： 对每个训练集训练一个基学习器（共 $T$ 个）。
3. 集成预测：
   • 分类： 使用 投票法 决定最终类别。
   • 回归： 使用 平均法 得到最终预测值。

特点：

• 简单直观，易于理解。
• 时间复杂度低。
• 适用于并行计算，可以同时训练多个基学习器。
• 降低方差，提高模型稳定性，不容易过拟合。
• 代表算法：随机森林 (Random Forest)

三、Boosting

1. 初始化： 基于初始训练集训练一个基学习器，并初始化样本权重。
2. 迭代训练：
   • 根据基学习器的表现 调整样本权重，增加被错误分类样本的权重，降低被正确分类样本的权重。
   • 基于调整后的训练集（样本权重）训练下一个基学习器。
3. 重复步骤 2，直到基学习器数量达到预设值或满足其他停止条件。
4. 加权结合： 将所有基学习器根据其 权重 进行加权结合，得到最终的强学习器。

特点：

• 相比 Bagging 更具 目的性，专注于被错误分类的样本。
• 降低偏差，提高模型精度。
• 可能增加方差，容易过拟合（需要控制迭代次数和正则化）。
• 代表算法：AdaBoost, Gradient Boosting (GBDT), XGBoost, LightGBM

四、AdaBoost (Adaptive Boosting)

1. 数据： 给定一个二分类数据集。
2. 过程： 通过寻找直线方程来将两类点区分开。
3. 每一轮迭代：
   • 根据当前样本权重训练基学习器。
   • 计算基学习器的 误差率 $e_i$。
   • 计算基学习器的 权重系数 $\alpha_i = \frac{1}{2} \log \frac{1 - e_i}{e_i}$。
   • 更新样本权重：
     • 误分类样本： 权重增大。
     • 正确分类样本： 权重减小。
4. 最终分类器： $H_{final}(x) = \text{sign}\left(\sum_{i=1}^M \alpha_i h_i(x)\right)$，其中 $h_i(x)$ 是第 $i$ 个基学习器。

关键点：

• 误差率越小，基学习器权重越大。
• 误分类样本在下一轮训练中更受关注。

五、其他补充

• 基学习器的选择：
  • Bagging： 通常选择 不稳定 的学习器，如决策树、神经网络。
  • Boosting： 通常选择 简单 的学习器，如决策树桩 (decision stump)。
• 结合策略： 除了投票法和平均法，还有学习法（例如 Stacking）。
• 多样性： 集成模型的效果很大程度上取决于基学习器的 多样性。可以通过不同的训练数据、不同的算法、不同的参数等方式来增加多样性。

好的，以下是一份完整的聚类复习笔记，整合了之前的内容，力求全面、严谨且易于理解：

聚类 (Clustering) 复习笔记

一、什么是聚类？

• 定义： 聚类是一种 无监督学习 方法，旨在将数据集中的样本划分为若干个 互不相交 的子集，每个子集称为一个 簇 (cluster)。
• 目标： 使得 簇内样本相似度高，簇间样本相似度低。
• 应用：
  • 作为单独过程，用于 发现数据内在分布结构。
  • 作为其他任务（如分类）的 前驱过程。

二、聚类问题的核心要素

1. 性能度量 (Performance Measure)： 评估聚类结果好坏的指标。
2. 距离计算 (Distance Calculation)： 定义样本之间的 相似性/相异性。
3. 聚类策略 (Clustering Strategy)： 寻找簇划分的 算法。

三、性能度量

用于评估聚类结果的优劣，好的聚类结果应该 簇内相似度高 且 簇间相似度低。

• 内部指标 (Internal Index)： 仅依赖于聚类结果和数据集本身，不使用任何外部信息。
  • Davies-Bouldin Index (DBI)： 值越 小 越好。（簇间相似度低）
    • 计算每个簇与其他簇之间的平均相似度，并取最大值。
    • $DBI = \frac{1}{k} \sum_{i=1}^{k} \max_{j \neq i} \left( \frac{avg(C_i) + avg(C_j)}{d_{cen}(\mu_i, \mu_j)} \right)$
    • 其中：
      • $k$ 是簇的数量。
      • $avg(C_i)$ 是簇 $C_i$ 内样本的平均距离。
      • $d_{cen}(\mu_i, \mu_j)$ 是簇 $C_i$ 和 $C_j$ 中心点之间的距离。
  • Dunn Index (DI)： 值越 大 越好。
    • 计算任意两个簇之间最近样本的距离除以任意簇内样本的最远距离，并取最小值。
    • $DI = \min_{1 \le i \le k} \left{ \min_{j \neq i} \left( \frac{d_{min}(C_i, C_j)}{\max_{1 \le l \le k} diam(C_l)} \right) \right}$
    • 其中：
      • $d_{min}(C_i, C_j)$ 是簇 $C_i$ 和 $C_j$ 最近样本对之间的距离。
      • $diam(C_l)$ 是簇 $C_l$ 内样本间的最远距离。
• 外部指标 (External Index)： 将聚类结果与某个 参考模型 或 真实标签 进行比较。
  • Jaccard Coefficient (JC)： 值越 大 越好。
  • FM Index (FMI)： 值越 大 越好。
  • Rand Index (RI)： 值越 大 越好。
  • 这些指标都基于对样本对的计数，考虑聚类结果和参考模型中样本对的对应关系。

四、距离计算

• 核心思想： 衡量样本之间的相似性或相异性。
• 常见距离度量：
  • 闵可夫斯基距离 (Minkowski distance)：

    • $dist(x_i, x_j) = (\sum_{u=1}^{n}

      x_{iu} - x_{ju}

      ^p)^{1/p}$

    • 当 $p=2$ 时，退化为 欧氏距离 (Euclidean distance)。
    • 当 $p=1$ 时，退化为 曼哈顿距离 (Manhattan distance)。
  • 余弦距离 (Cosine distance)：

    • $dist(x_i, x_j) = 1 - \frac{x_i \cdot x_j}{

      x_i

      \cdot

      x_j

      }$

    • 适用于文本相似度等场景。
  • 汉明距离 (Hamming Distance)： 用于 离散值（标称属性）。
    • 定义： 两个等长字符串对应位置的不同字符的个数。
    • 应用： K-Modes 聚类。
    • 示例： “1011101” 与 “1001001” 的汉明距离为 2。
  • 马氏距离 (Mahalanobis Distance)： 考虑 特征之间的相关性。
    • 定义： $D_M(x) = \sqrt{(x - \mu)^T \Sigma^{-1} (x - \mu)}$，其中 $\mu$ 是样本均值向量，$\Sigma$ 是协方差矩阵。
    • 特点：
      • 消除了不同特征之间量纲的影响。
      • 考虑了特征之间的相关性，更准确地反映样本之间的相似度。
      • 对一个样本点来说，马氏距离是关于协方差矩阵的距离。
    • 与欧氏距离的关系： 当协方差矩阵为单位矩阵时，马氏距离退化为欧氏距离。
  • 搬土距离/EMD (Earth Mover’s Distance)： 用于衡量两个概率分布之间的距离，可以理解为将一个分布“搬运”成另一个分布所需的最小代价。
    • 定义： $W[P_r, P_\theta] = \inf_{\gamma \in \Pi[P_r, P_\theta]} \int \int \gamma(x, y) d(x, y) dx dy$
      • $P_r$：原始分布。
      • $P_\theta$：目标分布。
      • $\gamma(x, y)$：从 $x$ 搬运到 $y$ 的“土”的量。
      • $d(x, y)$：搬运单位“土”的距离。
      • $\Pi[P_r, P_\theta]$：所有可能的联合分布的集合。
    • 工作量： 单位泥土的总量乘以它移动的距离。
    • 特点：
      • 适用于衡量两个分布之间的相似度。
      • 可以用于图像检索、文本相似度计算等领域。

如何对异构特征进行合理的距离度量？

• 异构特征： 指同时包含连续属性和离散属性的特征。
• 方法： 分别采用欧氏距离和汉明距离，再用加权融合。
  • K-Prototype 聚类：
    • $dist(x_i, x_j) = \sqrt{\sum_{l=1}^{n_c} (x_{il}^c - x_{jl}^c)^2 + \gamma_l \sum_{l=1}^{n_d} \delta(x_{il}^d, x_{jl}^d)}$
    • 其中：
      • $n_c$ 是连续属性的数量。
      • $n_d$ 是离散属性的数量。
      • $x_{il}^c$ 表示样本 $x_i$ 在第 $l$ 个连续属性上的取值。
      • $x_{il}^d$ 表示样本 $x_i$ 在第 $l$ 个离散属性上的取值。
      • $\delta(x_{il}^d, x_{jl}^d)$ 当 $x_{il}^d = x_{jl}^d$ 时为 0，否则为 1。
      • $\gamma_l$ 是权重，用于平衡连续属性和离散属性的重要性。

五、常用聚类算法

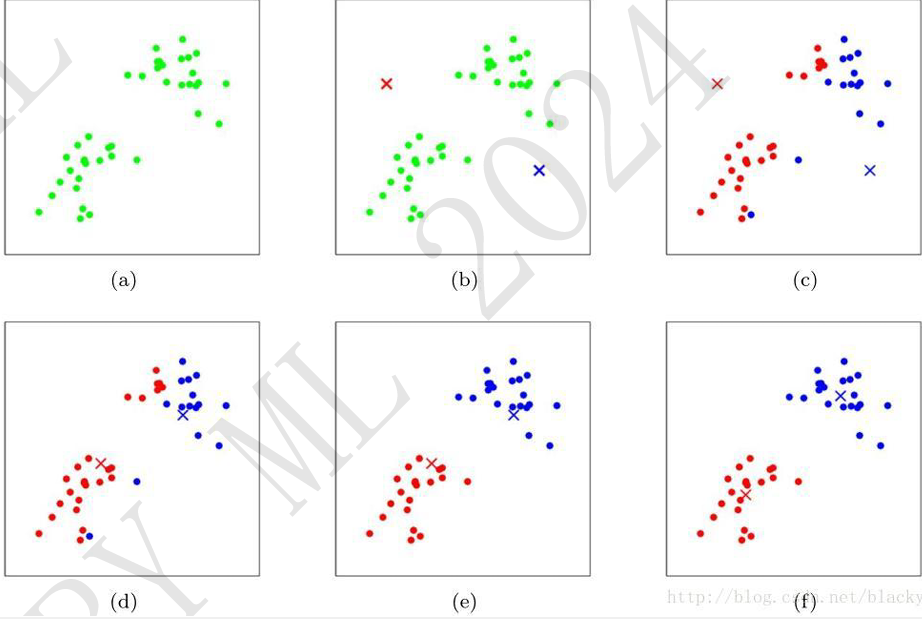
1. K-均值 (K-Means)

   • 算法步骤：
     1. 选择 K 值： 确定要生成的簇的数量。
     2. 初始化： 随机选择 K 个样本作为初始 簇中心。
     3. 划分样本： 将每个样本分配到与其最近的簇中心所属的簇。
     4. 更新簇中心： 重新计算每个簇的中心（通常是簇内样本的均值）。
     5. 重复步骤 3 和 4，直到簇中心不再发生变化或达到最大迭代次数。

     

   • 特点：
     • 简单、高效，是最常用的聚类算法之一。
     • 对初始簇中心敏感，可能会收敛到局部最优解。
     • 需要预先指定簇的数量 K。
     • 适用于簇结构为凸形、大小相似且方差相近的数据集。

2. DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

   • 核心概念： 基于 密度 的聚类，将簇定义为 密度相连 的样本点的集合。
   • 参数：
     • $\epsilon$ (eps)： 邻域半径。
     • MinPts： 邻域内样本点的最小数量。
   • 点的类型：
     • 核心点 (Core point)： $\epsilon$-邻域内至少包含 MinPts 个样本点。
     • 边界点 (Border point)： $\epsilon$-邻域内样本点数量少于 MinPts，但落在某个核心点的邻域内。
     • 噪声点 (Noise point)： 既不是核心点也不是边界点。
   • 密度相关定义：
     • 密度直达 (Directly density-reachable)： 样本点 $x_j$ 在 $x_i$ 的 $\epsilon$-邻域内，且 $x_i$ 是核心点，则称 $x_j$ 由 $x_i$ 密度直达。
     • 密度可达 (Density-reachable)： 存在一个样本序列 $p_1, p_2, \dots, p_t$，其中 $p_1 = x_i$, $p_t = x_j$，且 $p_{t+1}$ 由 $p_t$ 密度直达，则称 $x_j$ 由 $x_i$ 密度可达。
     • 密度相连 (Density-connected)： 存在一个核心点 $x_k$，使得 $x_i$ 和 $x_j$ 均由 $x_k$ 密度可达，则称 $x_i$ 和 $x_j$ 密度相连。
   • 算法步骤：
     1. 从数据集中随机选择一个未被处理的点。
     2. 如果该点是核心点，则创建一个新的簇，并将所有与该点密度可达的点加入该簇。
     3. 如果该点是边界点，则暂时将其标记为噪声点，并继续处理下一个点。
     4. 重复步骤 1-3，直到所有点都被处理。
   • 特点：
     • 无需预先指定簇的数量。
     • 可以发现任意形状的簇。
     • 能够识别噪声点。
     • 对参数 $\epsilon$ 和 MinPts 敏感。
     • 对于密度不均匀、聚类间距差别很大的数据集，聚类质量较差。

六、聚类策略

1. 划分式 (Partitional) 聚类： 将样本划分为若干个不相交的子集（簇）。
   • 特点： 通常需要预先指定簇的数量。
   • 算法： K-Means, DBSCAN, 谱聚类 (Spectral Clustering) 等。
2. 分层式 (Hierarchical) 聚类： 将相似的样本逐渐汇聚成更大的簇，直到所有样本被汇入一个簇，或达到预设的终止条件。

聚类策略比较：

特性	划分式	分层式
簇数量	通常需要预先指定	无需预先指定
时间复杂度	通常较低	通常较高 ($O(n^2)$)
簇分布规律	探究样本的簇分布规律	探究样本分布的相似性嵌套规律
与划分式聚类结合	可用于加速分层式聚类过程	可对分层聚类结果的树状结构进行横切获得划分式聚类结果
典型算法	K-Means, DBSCAN, 谱聚类	凝聚式聚类, 分裂式聚类

机器学习特征工程笔记

一、什么是特征工程？

• 定义： 特征工程是指利用领域知识从原始数据中提取、构建、转换或选择特征的过程，以便更好地服务于机器学习模型。
• 俗语： 数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。
• 目标： 最大限度地从原始数据中提取有用信息，构建出 高质量的特征，以提升模型的性能。

二、特征工程的主要内容

特征工程主要包括两大类：

1. 降维 (Dimension Reduction) ：在保留重要信息的前提下，减少特征的数量，降低数据的维度。
2. 特征选择 (Feature Selection) ：从原始特征集合中挑选出 最有用 的特征子集。

三、降维

• 目的：
  • 降低计算复杂度。
  • 减少存储空间。
  • 去除冗余信息，避免过拟合。
  • 方便数据可视化。
• 常见方法：
  • 主成分分析 (Principal Component Analysis, PCA)：
    • 核心思想： 将原始数据投影到 方差最大 的几个方向（主成分）上，以此保留数据的主要信息。
    • 通俗理解： 找到数据中最主要的几个变化方向，用这些方向来表示数据。
    • 优点： 无监督学习方法，不需要标签信息。
    • 缺点： 解释性不如原始特征。
  • 线性判别分析 (Linear Discriminant Analysis, LDA)：
    • 核心思想： 将数据投影到能 最好地区分不同类别 的方向上。
    • 通俗理解： 找到一个投影方向，使得不同类别的数据在这个方向上尽可能分开，相同类别的数据尽可能聚集。
    • 优点： 有监督学习方法，利用了标签信息，通常能获得比 PCA 更好的分类性能。
    • 缺点： 需要标签信息，且对数据分布有一定的假设。
  • PCA vs. LDA：
    • 联系： 两者都是常用的降维方法，都通过线性变换将数据投影到低维空间。
    • 区别： PCA 关注数据的 方差，LDA 关注 类别可分性；PCA 是 无监督 的，LDA 是 有监督 的。
  • 多维缩放 (Multidimensional Scaling, MDS)：
    • 核心思想： 尽可能地保留样本点在原始空间中的 距离关系。
    • 通俗理解： 在低维空间中重新排列样本点，使得它们之间的距离关系与在高维空间中尽可能相似。
    • 优点： 可以用于非线性数据的降维。
    • 缺点： 计算复杂度较高。

四、特征选择

• 目的：
  • 减轻维度灾难： 特征过多会增加计算负担，降低模型效率。
  • 去除无关或冗余特征： 保留携带关键信息的特征，降低学习难度，提高模型性能。
• 主要方法：
  • 过滤式 (Filter)： 先对特征进行评估和排序，再选择特征，与后续学习器无关。
    • 核心思想： 评估每个特征的 重要性 或 相关性，然后选择得分高的特征。
    • 通俗理解： 类似于“海选”，先根据一些指标对特征进行打分，然后选出得分高的特征。
    • 优点： 计算效率高，速度快。
    • 缺点： 可能选出的不是最优的特征组合，因为没有考虑与后续学习器的关系。
    • 常见方法：
      • 方差选择法： 移除方差低于阈值的特征（方差很小的特征通常信息量较少）。
      • 相关系数法： 计算特征与目标变量之间的相关系数，选择相关性强的特征。
      • 互信息法： 衡量特征与目标变量之间的互信息，选择互信息大的特征。
      • 卡方检验： 用于分类问题，衡量特征与类别之间的独立性，选择独立性弱的特征（即与类别相关的特征）。
    • 是否适用于有监督/无监督任务？
      • 方差选择法可以用于 无监督 任务（因为它只考虑特征本身的方差）。
      • 相关系数法、互信息法和卡方检验通常用于 有监督 任务（因为它们需要目标变量的信息）。
  • 包裹式 (Wrapper)： 将 后续学习器的性能 作为特征子集的评价标准。
    • 核心思想： 将特征选择看作是一个搜索问题，通过不同的搜索策略找到最优的特征子集，使得模型在该特征子集上的性能最好。
    • 通俗理解： 类似于“选拔”，直接用模型在不同的特征子集上进行训练和评估，选择效果最好的特征子集。
    • 优点： 通常能获得比过滤式方法更好的性能，因为考虑了与后续学习器的关系。
    • 缺点： 计算复杂度高，特别是当特征数量很多时。
    • 常见方法：
      • 递归特征消除 (Recursive Feature Elimination, RFE)： 反复构建模型，每次删除最不重要的特征，直到达到指定的特征数量。

五、总结

特征工程是机器学习中至关重要的一步，好的特征工程可以显著提升模型的性能。特征工程主要包括降维和特征选择两大类。降维旨在减少特征数量，降低数据维度；特征选择旨在挑选出最有用的特征子集。选择合适的方法需要根据具体的数据和任务来决定。

---

速通神经网络

一、神经网络基础：神经元与感知机

• 神经元 (Neuron)：

  神经网络的基本组成单元，模拟生物神经元的工作原理。

  • 结构： 接收多个输入信号 $x_i$，对每个输入信号乘以一个权重 $w_i$，然后将所有加权输入求和 $\sum_{i=1}^{n} w_i x_i$，加上一个偏置项 $b$，最后通过一个激活函数 $f$ 得到输出 $y = f(\sum_{i=1}^{n} w_i x_i + b)$。
  • 通俗理解： 神经元就像一个打分器，对每个输入信号根据其重要性（权重）打分，然后综合所有得分（加权求和），加上一个基准分（偏置），最后根据一个规则（激活函数）输出最终结果。
  • 数学表示： $y = f(\sum_{i=1}^{n} w_i x_i + b)$，其中 $x_i$ 是输入，$w_i$ 是权重，$b$ 是偏置，$f$ 是激活函数，$y$ 是输出。
  • 权重和偏置的意义：
    • 权重 ($w_i$)： 表示输入信号的重要性，权重越大，表示该输入信号对输出的影响越大。
    • 偏置 ($b$)： 表示神经元的激活阈值，偏置越大，神经元越不容易被激活。

• 激活函数 (Activation Function)：

  引入非线性因素，增强模型的表达能力，使得神经网络可以逼近任意复杂的非线性函数。

  • 为什么需要非线性激活函数？
    • 如果使用线性激活函数，无论神经网络有多少层，输出都是输入的线性组合，这样的网络只能解决线性问题，无法解决非线性问题。
    • 非线性激活函数可以引入非线性因素，使得神经网络可以逼近任意复杂的非线性函数。
  • 常见激活函数：
    • Sigmoid: 将输入映射到 (0, 1) 之间，常用于二分类问题。公式：$\sigma(x) = \frac{1}{1 + e^{-x}}$。特点： 输出值在 (0, 1) 之间，可以将输出解释为概率；缺点： 容易出现梯度消失问题，当输入值非常大或非常小时，梯度接近于 0，导致参数更新缓慢。
    • Tanh: 将输入映射到 (-1, 1) 之间，是 Sigmoid 的变体。公式：$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$。特点： 输出值在 (-1, 1) 之间，数据中心化，收敛速度比 Sigmoid 快；缺点： 仍然存在梯度消失问题。
    • ReLU (Rectified Linear Unit): 当输入大于 0 时，输出等于输入；当输入小于等于 0 时，输出为 0。目前最常用的激活函数之一。公式：$ReLU(x) = max(0, x)$。特点： 计算简单，收敛速度快；缺点： 容易出现“神经元死亡”问题，当输入小于 0 时，梯度为 0，导致参数无法更新。
    • Leaky ReLU: ReLU 的改进版，当输入小于 0 时，输出一个很小的负数，避免了“神经元死亡”问题。公式：$LeakyReLU(x) = max(\alpha x, x)$，其中 $\alpha$ 是一个很小的正数，例如 0.01。特点： 解决了 ReLU 的“神经元死亡”问题；缺点： 引入了一个新的超参数 $\alpha$。
    • Softmax: 用于多分类问题，将多个神经元的输出映射成一个概率分布。公式：$Softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}$。

• 感知机 (Perceptron)：

  最简单的神经网络模型，由一个神经元组成，可以用于解决线性可分的二分类问题。

  • 结构： 单层神经元结构，输入层直接连接到输出层。
  • 学习规则： 通过调整权重和偏置，使得感知机能够正确地对样本进行分类。
  • 算法步骤：
    1. 初始化权重和偏置。
    2. 选取一个训练样本 $(x, y)$。
    3. 计算感知机的输出 $\hat{y} = sign(\sum_{i=1}^{n} w_i x_i + b)$，其中 $sign$ 是符号函数。
    4. 如果 $\hat{y} \neq y$，则更新权重和偏置：$w_i = w_i + \eta (y - \hat{y}) x_i$，$b = b + \eta (y - \hat{y})$，其中 $\eta$ 是学习率。
    5. 重复步骤 2-4，直到所有样本都被正确分类或达到最大迭代次数。
  • 局限性： 无法解决非线性问题，例如异或 (XOR) 问题。这是因为感知机只能产生线性决策边界。

二、神经网络的学习方法：反向传播

• 前向传播 (Forward Propagation)： 输入信号从输入层经过隐藏层（如果有的话）传递到输出层，得到模型的预测结果。

• 反向传播 (Backpropagation)：

  • 核心思想： 根据模型的预测结果和真实标签之间的 误差，反向 逐层计算每个神经元权重的 梯度，然后根据梯度更新权重，使得误差减小。
  • 通俗理解： 类似于“复盘”，根据最终结果的偏差，反推每个环节（神经元）的贡献，然后调整每个环节的参数（权重），以改进最终结果。
  • 关键步骤：
    1. 计算损失函数（衡量模型预测结果与真实标签之间的差异）： 常用的损失函数有均方误差 (MSE)、交叉熵损失 (Cross-Entropy Loss) 等。
       • 均方误差 (MSE): $MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$，适用于回归问题。
       • 交叉熵损失 (Cross-Entropy Loss): $H(p, q) = -\sum_{i=1}^{n} p(x_i) \log q(x_i)$，其中 $p$ 是真实分布，$q$ 是预测分布，适用于分类问题。
    2. 计算损失函数对每个权重的梯度（使用链式法则）： 链式法则用于计算复合函数的导数。在神经网络中，损失函数是关于权重的复合函数，因此需要使用链式法则来计算损失函数对每个权重的梯度。
    3. 根据梯度更新权重（使用梯度下降法）： $w = w - \eta \frac{\partial L}{\partial w}$，其中 $w$ 是权重，$\eta$ 是学习率，$\frac{\partial L}{\partial w}$ 是损失函数对权重的梯度。

• 梯度下降 (Gradient Descent)：

  一种优化算法，用于寻找函数的最小值。在神经网络中，用于更新权重，使得损失函数最小化。

  • 原理： 沿着函数梯度的反方向更新参数，可以使函数值下降最快。
  • 变体：
    • 批量梯度下降 (Batch Gradient Descent)： 使用所有样本计算梯度。优点： 每次更新都能保证朝着全局最优的方向前进；缺点： 计算量大，训练速度慢。
    • 随机梯度下降 (Stochastic Gradient Descent)： 每次只使用一个样本计算梯度。优点： 计算量小，训练速度快；缺点： 容易陷入局部最优解，更新方向不稳定。
    • 小批量梯度下降 (Mini-batch Gradient Descent)： 使用一小批样本计算梯度，是前两者的折中。优点： 兼顾了训练速度和稳定性；缺点： 需要选择合适的批量大小。
  • 学习率 ($\eta$)： 控制每次更新的步长，学习率过大容易导致震荡，学习率过小会导致收敛速度慢。

三、深度神经网络 (Deep Neural Networks)

• 定义： 包含多个隐藏层的神经网络。
• 优点：
  • 更强的表达能力，可以学习更复杂的非线性关系。
  • 可以自动学习特征表示，无需人工设计特征。
• 挑战：
  • 容易过拟合：模型在训练集上表现很好，但在测试集上表现很差。解决方法： 正则化、Dropout、早停等。
  • 训练难度大，容易陷入局部最优解。解决方法： 使用更好的优化算法，例如 Adam、RMSprop 等；使用更好的初始化方法，例如 Xavier 初始化、He 初始化等。
  • 计算量大，需要大量的计算资源。解决方法： 使用 GPU 加速计算；使用更有效的网络结构，例如卷积神经网络、循环神经网络等。

四、深度生成网络 (Deep Generative Networks)

• 目标： 学习数据的潜在分布，并生成新的数据样本。
• 常见模型：
  • 变分自编码器 (Variational Autoencoder, VAE)：
    • 组成： 编码器 (Encoder) 和解码器 (Decoder)。
    • 原理： 编码器将输入数据编码成一个潜在向量 (Latent Vector)，解码器将潜在向量解码成重构数据。VAE 的目标是最小化重构误差，并使潜在向量的分布接近于一个先验分布（通常是标准正态分布）。
    • 特点： 可以生成新的数据样本，并且可以控制生成数据的属性。
  • 生成对抗网络 (Generative Adversarial Network, GAN)：
    • 组成： 生成器 (Generator) 和判别器 (Discriminator)。
    • 原理： 生成器生成假的数据样本，判别器判断输入样本是真实的还是假的。生成器和判别器相互对抗，不断提升自己的能力，最终生成器可以生成以假乱真的数据样本。
    • 特点： 可以生成高质量的数据样本，但训练不稳定，容易出现模式崩溃问题。

五、卷积神经网络 (Convolutional Neural Networks, CNNs)

• 特点： 专门用于处理具有 网格结构 的数据，例如图像。
• 核心组件：
  • 卷积层 (Convolutional Layer)： 使用 卷积核 提取局部特征。
    • 卷积核 (Kernel/Filter)： 一个小的矩阵，用于在输入数据上滑动，并计算卷积核与输入数据的对应元素的乘积之和。
    • 步长 (Stride)： 卷积核每次滑动的步长。
    • 填充 (Padding)： 在输入数据的周围填充 0，以控制输出特征图的大小。
    • 特征图 (Feature Map)： 卷积层的输出，表示输入数据在不同卷积核下的响应。
  • 池化层 (Pooling Layer)： 降低特征图的维度，减少计算量，并增强模型的鲁棒性。
    • 最大池化 (Max Pooling)： 选择池化窗口内的最大值作为输出。
    • 平均池化 (Average Pooling)： 计算池化窗口内的平均值作为输出。
• 优点：
  • 参数共享： 同一个卷积核可以用于提取不同位置的特征，减少了模型参数的数量。
  • 平移不变性： 对输入数据的平移具有一定的鲁棒性。例如，图像中的物体稍微移动了一下，CNN 仍然可以识别出该物体。
• 应用： 图像分类、目标检测、图像分割等。

六、循环神经网络 (Recurrent Neural Networks, RNNs)

• 特点： 专门用于处理 序列数据，例如文本、语音。
• 核心思想： 网络的隐藏状态会 循环 地传递到下一个时间步，从而捕捉序列中的 时序信息。
• 结构： RNN 的隐藏层会接收当前时间步的输入和上一个时间步的隐藏状态，并输出当前时间步的隐藏状态和输出。
• 公式：
  • $h_t = tanh(W_{xh}x_t + W_{hh}h_{t-1} + b_h)$
  • $o_t = W_{hy}h_t + b_y$
  • 其中，$x_t$ 是当前时间步的输入，$h_t$ 是当前时间步的隐藏状态，$h_{t-1}$ 是上一个时间步的隐藏状态，$o_t$ 是当前时间步的输出，$W_{xh}$、$W_{hh}$、$W_{hy}$ 是权重矩阵，$b_h$、$b_y$ 是偏置向量。
• 优点： 能够处理变长序列数据。
• 缺点： 容易出现梯度消失或梯度爆炸问题，难以训练。这是因为 RNN 的梯度在反向传播过程中会随着时间步的增加而指数级地衰减或增长。

七、长短期记忆网络 (Long Short-Term Memory Networks, LSTMs)

• 特点： RNN 的一种变体，通过引入 门控机制 来解决 RNN 的梯度消失或梯度爆炸问题。
• 核心组件：
  • 遗忘门 (Forget Gate)： 控制哪些信息需要被遗忘。$f_t = \sigma(W_{xf}x_t + W_{hf}h_{t-1} + b_f)$
  • 输入门 (Input Gate)： 控制哪些信息需要被添加到记忆单元中。$i_t = \sigma(W_{xi}x_t + W_{hi}h_{t-1} + b_i)$
  • 输出门 (Output Gate)： 控制哪些信息需要被输出。$o_t = \sigma(W_{xo}x_t + W_{ho}h_{t-1} + b_o)$
  • 记忆单元 (Cell State)： 存储长期信息。$c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}t$，其中 $\tilde{c}_t = tanh(W{xc}x_t + W_{hc}h_{t-1} + b_c)$
  • 隐藏状态 (Hidden State)： $h_t = o_t \odot tanh(c_t)$
  • 其中，$x_t$ 是当前时间步的输入，$h_t$ 是当前时间步的隐藏状态，$h_{t-1}$ 是上一个时间步的隐藏状态，$c_t$ 是当前时间步的记忆单元，$c_{t-1}$ 是上一个时间步的记忆单元，$f_t$、$i_t$、$o_t$ 分别是遗忘门、输入门和输出门的输出，$\sigma$ 是 Sigmoid 函数，$\odot$ 表示逐元素相乘，$W$ 和 $b$ 是权重矩阵和偏置向量。
• 优点： 能够学习长期依赖关系。LSTM 通过门控机制，可以选择性地记住或遗忘信息，从而解决了 RNN 的梯度消失或梯度爆炸问题，可以学习到序列数据中的长期依赖关系。
• 应用： 机器翻译、文本生成、语音识别等。

计算智能

一、遗传算法 (Genetic Algorithm, GA)

• 核心思想： 模拟生物进化中的“自然选择”和“遗传变异”机制，通过迭代的方式搜索最优解。
• 关键概念：
  • 基因 (Gene)： 问题的解的编码表示，通常是一个二进制串或实数向量。
  • 个体 (Individual)： 一个可能的解，由一组基因组成。
  • 种群 (Population)： 一组个体的集合。
  • 适应度函数 (Fitness Function)： 评估个体优劣的函数，适应度越高，个体越优秀。
  • 选择 (Selection)： 根据个体的适应度，选择优秀的个体进入下一代。常用的选择算子有轮盘赌选择、锦标赛选择等。
  • 交叉 (Crossover)： 将两个个体的基因进行交换，产生新的个体。
  • 变异 (Mutation)： 以一定的概率改变个体的某个基因，引入新的基因组合。
• 算法流程：
  1. 初始化种群。
  2. 计算每个个体的适应度。
  3. 选择：根据适应度选择个体进入下一代。
  4. 交叉：对选出的个体进行交叉操作，产生新的个体。
  5. 变异：对新的个体进行变异操作。
  6. 重复步骤 2-5，直到满足终止条件（例如达到最大迭代次数或找到满足要求的解）。
• 优点：
  • 全局搜索能力强，不易陷入局部最优解。
  • 可并行化，适合解决大规模优化问题。
  • 对问题的形式没有严格要求，适用范围广。
• 缺点：
  • 算法参数较多，需要仔细调整。
  • 收敛速度较慢，计算量较大。
• 应用： 函数优化、组合优化、机器学习模型参数调优等。

二、蚁群算法 (Ant Colony Optimization, ACO)

• 核心思想： 模拟蚂蚁觅食的行为，通过信息素的积累和挥发来引导搜索方向，最终找到最优路径。
• 关键概念：
  • 信息素 (Pheromone)： 蚂蚁在路径上留下的化学物质，用于指导其他蚂蚁的行为。信息素浓度越高，表示该路径越优。
  • 信息素挥发 (Pheromone Evaporation)： 信息素会随着时间的推移而挥发，避免算法过早收敛到局部最优解。
  • 路径选择 (Path Selection)： 蚂蚁根据路径上的信息素浓度和启发式信息（例如距离）来选择下一步要走的路径。
• 算法流程：
  1. 初始化信息素。
  2. 每只蚂蚁根据信息素和启发式信息构建路径。
  3. 计算每条路径的长度。
  4. 更新信息素：在较短的路径上增加信息素，所有路径上的信息素都会挥发一部分。
  5. 重复步骤 2-4，直到满足终止条件。
• 优点：
  • 分布式计算，具有较强的鲁棒性和自适应性。
  • 易于与其他算法结合。
• 缺点：
  • 收敛速度较慢，容易出现停滞现象。
  • 参数设置对算法性能影响较大。
• 应用： 旅行商问题 (TSP)、车辆路径问题 (VRP)、作业调度问题等。

三、强化学习 (Reinforcement Learning, RL)

• 核心思想： 智能体 (Agent) 通过与环境 (Environment) 交互，学习在不同状态 (State) 下采取何种动作 (Action) 可以最大化累积奖励 (Reward)。
• 关键概念：
  • 智能体 (Agent)： 能够感知环境并做出决策的实体。
  • 环境 (Environment)： 智能体所处的外部世界。
  • 状态 (State)： 描述环境当前状况的信息。
  • 动作 (Action)： 智能体可以采取的行为。
  • 奖励 (Reward)： 环境对智能体采取的动作的反馈，可以是正的、负的或零。
  • 策略 (Policy)： 智能体根据当前状态选择动作的规则。
  • 价值函数 (Value Function)： 评估当前状态或状态-动作对的价值，表示未来可以获得的累积奖励的期望。
• 学习目标： 学习一个最优策略，使得智能体在与环境交互的过程中能够获得最大的累积奖励。
• 常见算法：
  • Q-learning： 一种基于价值的强化学习算法，通过学习状态-动作价值函数 (Q 函数) 来找到最优策略。
  • SARSA： 一种在线的 (on-policy) 强化学习算法，与 Q-learning 类似，但更新 Q 函数的方式不同。
  • Deep Q-Network (DQN)： 将深度学习与 Q-learning 结合，使用神经网络来近似 Q 函数。
• 优点：
  • 能够解决复杂的序列决策问题。
  • 无需人工标注数据，可以从与环境的交互中学习。
• 缺点：
  • 训练过程不稳定，容易受到奖励函数设计的影响。
  • 样本效率低，需要大量的交互数据才能学习到好的策略。
• 应用： 游戏 AI、机器人控制、自动驾驶等。

四、智能规划 (Intelligent Planning)

• 定义： 研究如何使计算机能够自动生成一系列动作，以实现特定目标。
• 核心问题： 状态空间搜索。
• 常见方法：
  • 基于搜索的规划： 使用搜索算法（例如 A* 算法）在状态空间中搜索一条从初始状态到目标状态的路径。
  • 基于逻辑的规划： 使用逻辑推理来推导出实现目标的动作序列。
  • 分层规划： 将复杂问题分解成多个子问题，分别进行规划，然后将子问题的解组合成最终的解决方案。
• 应用： 机器人导航、任务调度、物流规划等。

五、迁移学习 & 联邦学习 (Transfer Learning & Federated Learning)

• 迁移学习 (Transfer Learning)：
  • 核心思想： 将在一个任务上学习到的知识迁移到另一个相关的任务上，以提高学习效率和性能。
  • 关键概念：
    • 源域 (Source Domain)： 拥有大量已标注数据的领域。
    • 目标域 (Target Domain)： 只有少量或没有已标注数据的领域。
  • 方法：
    • 基于实例的迁移 (Instance-based Transfer Learning)： 重用源域中的数据实例。
    • 基于特征的迁移 (Feature-based Transfer Learning)： 学习一个通用的特征表示，可以用于源域和目标域。
    • 基于模型的迁移 (Model-based Transfer Learning)： 重用源域中训练好的模型参数，并在目标域上进行微调。
  • 优点：
    • 减少对目标域数据的依赖。
    • 加快目标域任务的学习速度。
    • 提高目标域任务的性能。
  • 应用： 图像分类、目标检测、自然语言处理等。
• 联邦学习 (Federated Learning)：
  • 核心思想： 在多个分散的数据集上训练一个共享的模型，同时保护数据隐私。
  • 关键概念：
    • 客户端 (Client)： 拥有本地数据的设备或机构。
    • 服务器 (Server)： 协调模型的训练过程。
  • 算法流程：
    1. 服务器将当前模型参数发送给客户端。
    2. 客户端使用本地数据训练模型，并计算模型参数的更新。
    3. 客户端将模型参数的更新发送给服务器。
    4. 服务器聚合客户端的更新，并更新全局模型参数。
    5. 重复步骤 1-4，直到模型收敛。
  • 优点：
    • 保护数据隐私，数据不出本地。
    • 可以利用分散的数据进行模型训练。
  • 挑战：
    • 通信开销大。
    • 数据异构性。
    • 模型安全性。
  • 应用： 移动设备输入法预测、医疗数据分析、金融风控等。