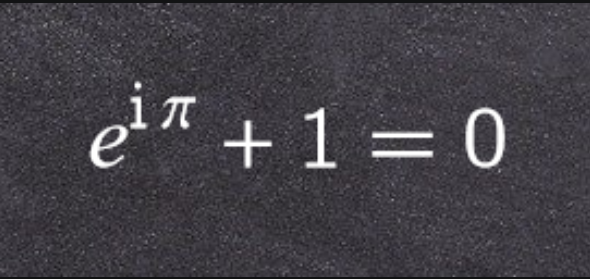Post

【待完善】Markdown 数学公式格式

数学公式如何显示在MD文档中？

Posted
Preview Image
By Zwei
10 min read
【待完善】Markdown 数学公式格式

一、常用符号

内联公式

在 Markdown 语法中可以书写数学公式，书写数学公式必须要有一个入口——内联公式。

1

$ 数学公式 $

即一对美元符号将所要书写的数学公式括起来就可以让编辑器识别并预览。一对美元符号对应一行数学公式，多行数学公式就需要两对美元符号。

1
2
3
4
5
6
7
8

$$
数学公式\ =\  
\begin{cases}
数学公式\\
数学公式\\
数学公式\\
\end{cases}
$$
\[数学公式\ =\ \begin{cases} 数学公式\\ 数学公式\\ 数学公式\\ \end{cases}\]

其中，编辑器默认一对 {} 符号内的内容为一个整体，以斜线 \ 加空格表示空格，双斜线 \\ 表示换行。

常用符号

名称 实例 预览 注释
上下标 a^n_m   上标^用于指数，下标用于角标
正负号（±） a \pm b a±b  
乘 \times ×  
除 \div ÷  
根号 \sqrt   根号下(a-b)
大于 \gt ＞  
小于 \lt ＜  
大于等于 \ge ≥  
小于等于 \le ≤  
正无穷 \infty ∞  
负无穷 -\infty -∞  
分数 \dfrac{a}   a分之b
省略号 \cdots …  

三角函数

数学表达式 代码
sinθ \sin
cosθ \cos
tanθ \tan
cotθ \cot

矢量、累加累乘、极限

数学表达式 代码
矢量 \vec{}
累加（求和∑） \sum_{}^{}
累乘（求积∏） \prod_{}^{}
极限 \lim_{}

希腊字母表

代码 预览 代码 预览
\alpha α \pi π
\beta β \rho ρ
\gamma γ \xi ξ
\delta δ \nu ν
\epsilon ϵ \upsilon υ
\varepsilon ε \varphi φ
\eta η \chi χ
\theta θ \psi ψ
\kappa κ \omega ω
\iota ι \Omega Ω
\zeta ζ \Gamma Γ
\lambda λ \Delta Δ
\mu μ    
\phi φ \Phi Φ

矩阵

简单矩阵

简单矩阵示例1

使用 \begin{matrix} ... \end{matrix} 生成，每一行以 \\ 结尾表示换行，各元素间以 & 隔开，右边的数学公式代码块序号用 \tag{n} 表示。

\[\begin{matrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{matrix} \tag{简单矩阵 - 示例1}\] 
1
2
3
4
5
6
7
8

$$
\begin{matrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{matrix}
\tag{简单矩阵 - 示例1}
$$

简单矩阵示例二（带括号）

大括号
\[\left\{ \begin{matrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{matrix} \right\} \tag{带有大括号的矩阵}\] 
1
2
3
4
5
6
7
8
9
10

$$
\left\{
\begin{matrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{matrix}
\right\}
\tag{带有大括号的矩阵}
$$

或

\[\begin{Bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{Bmatrix} \tag{6}\] 
1
2
3
4
5
6
7
8

$$
\begin{Bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{Bmatrix}
\tag{6}
$$
中括号
\[\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \tag{中括号}\] 
1
2
3
4
5
6
7
8
9
10

$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix}
\right]
\tag{中括号}
$$

或

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \tag{6}\] 
1
2
3
4
5
6
7
8

$$
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix}
\tag{6}
$$
小括号
\[\left( \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right) \tag{小括号}\] 
1
2
3
4
5
6
7
8
9
10

$$
\left(
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix}
\right)
\tag{小括号}
$$
包含省略号和希腊字母

行省略号 \cdots，列省略号 \vdots，斜向省略号（左上至右下） \ddots。

\[\left\{ \begin{matrix} 1 & 2 & \cdots & 5 \\ 6 & 7 & \cdots & 10 \\ \vdots & \vdots & \ddots & \vdots \\ \alpha & \alpha+1 & \cdots & \alpha+4 \end{matrix} \right\}\] 
1
2
3
4
5
6
7
8
9
10

$$
\left\{
\begin{matrix}
1      & 2        & \cdots & 5        \\
6      & 7        & \cdots & 10       \\
\vdots & \vdots   & \ddots & \vdots   \\
\alpha & \alpha+1 & \cdots & \alpha+4 
\end{matrix}
\right\}
$$

表格

简单表格

开头结尾：

1

\begin{array} ... \end{array}

定义式：

例：{|c|c|c|}，其中 c l r 分别代表居中、左对齐及右对齐。

分割线：

  1. 竖直分割线：在定义式中插入 |， （|| 表示两条竖直分割线）。
  2. 水平分割线：在下一行输入前插入 \hline，以下图真值表为例。

其他：每行元素间均须要插入 & ，每行元素以 \\ 结尾。

\[\begin{array}{|c|c|c|} \hline 2&9&4\\ \hline 7&5&3\\ \hline 6&1&8\\ \hline \end{array}\] 
1
2
3
4
5
6
7
8

$$
\begin{array}{|c|c|c|}
\hline 2&9&4\\
\hline 7&5&3\\
\hline 6&1&8\\
\hline
\end{array}
$$

真值表

\[\begin{array}{cc|c} A & B & F \\ \hline 0 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}\] 
1
2
3
4
5
6
7
8
9

$$
\begin{array}{cc|c}
A & B & F \\
\hline 0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\
\end{array}
$$

方程组、表达条件式

方程组

\[\begin{cases} 3x + 5y + z \\ 7x - 2y + 4z \\ -6x + 3y + 2z \end{cases}\] 
1
2
3
4
5
6
7

$$
\begin{cases}
3x + 5y + z \\
7x - 2y + 4z \\
-6x + 3y + 2z
\end{cases}
$$

表达条件式/分段函数

\[f(n) = \begin{cases} n/2, & \text{if } n \text{ is even} \\ 3n+1, & \text{if } n \text{ is odd} \end{cases}\] 
1
2
3
4
5
6
7

$$
f(n) =
\begin{cases} 
n/2, & \text{if } n \text{ is even} \\
3n+1, & \text{if } n \text{ is odd}
\end{cases}
$$

格式

代码块内多行代码对齐

\[\begin{aligned} a &= b + c \\ &= d + e + f \end{aligned}\] 
1
2
3
4
5
6

$$
\begin{aligned}
a &= b + c \\
  &= d + e + f
\end{aligned}
$$

间隔（空格、跟随）

跟随 \!

无空格 小空格 \, 中空格 \; 大空格 \

真空格 \quad 双真空格 \qquad

\[a\!b + ab + a\,b + a\;b + a\ b + a\quad b + a\qquad b\] 
1
2
3

$$
a\!b + ab + a\,b + a\;b + a\ b + a\quad b + a\qquad b
$$

箭头符号

表达式 预览
\uparrow ↑
\downarrow ↓
\Uparrow ⇑
\Downarrow ⇓
\rightarrow →
\leftarrow ←
\Rightarrow ⇒
\Leftarrow ⇐
\longrightarrow ⟶
\longleftarrow ⟵
\Longrightarrow ⟹
\Longleftarrow ⟸

逻辑运算符

表达式 预览
\because ∵
\therefore ∴
\forall ∀
\exists ∃
\not= ≠
\not> ≯
\not\subset ⊄

微积分运算符

表达式 预览
\prime ′
\int ∫
\iint ∬
\iiint ∭
\oint ∮
\lim lim
\infty ∞
\nabla ∇

三角运算符

表达式 预览
\bot ⊥
\angle ∠
\sin sin
\cos cos
\tan tan
\cot cot
\sec sec
\csc csc

希腊字母

表达式 预览 表达式 预览
\alpha α \beta β
\gamma γ \delta δ
\epsilon ϵ \zeta ζ
\eta η \theta θ
\iota ι \kappa κ
\lambda λ \mu μ
\nu ν \xi ξ
\pi π \rho ρ
\sigma σ \tau τ
\upsilon υ \phi ϕ
\chi χ \psi ψ
\omega ω \Gamma Γ
\Delta Δ \Theta Θ
\Lambda Λ \Xi Ξ
\Pi Π \Sigma Σ
\Upsilon Υ \Phi Φ
\Psi Ψ \Omega Ω

关系运算符

表达式 预览 表达式 预览
\pm ± \times ×
\div ÷ \mid ∣
\nmid ∤ \cdot ⋅
\circ ∘ \ast ∗
\leq ≤ \geq ≥
\neq ≠ \approx ≈
\equiv ≡ \sum ∑
\prod ∏ \coprod ∐

集合运算符

表达式 预览 表达式 预览
\emptyset ∅ \in ∈
\notin ∉ \subset ⊂
\supset ⊃ \subseteq ⊆
\supseteq ⊇ \bigcap ⋂
\bigcup ⋃ \bigvee ⋁
\bigwedge ⋀ \biguplus ⨄
\bigsqcup ⨆    

对数运算符

表达式 预览
\log log
\lg lg
\ln ln

更多数学符号

上标与下标

上标：$x^2$, $A^{上标}$
下标：$x_2$, $A_{下标}$

分数与开方

分数：$\frac{a}{b}$, $\dfrac{2}{3}$
开方：$\sqrt{x}$, $\sqrt[3]{x}$

积分与极限

积分：$\int_0^2 x^2 \, \mathrm{d}x$
极限：$\lim_{n \rightarrow +\infty} \frac{1}{n(n+1)}$

矢量与累加累乘

矢量：$\vec{a}$
累加：$\sum_{i=0}^n \frac{1}{i^2}$
累乘：$\prod_{i=0}^n \frac{1}{i^2}$

戴帽符号

表达式 预览
\hat{x} ^x
\check{x} ˇx
\breve{x} ˘x
\bar{x} ¯x
\tilde{x} ~x
\widetilde{X} ˜X
\vec{x} →x
\dot{x} ˙x
\ddot{x} ¨x

连线符号

表达式 预览
\overline{a+b+c+d} \(\overline{a+b+c+d}\)
\underline{a+b+c+d} \underline{a+b+c+d}
\overbrace{a+\underbrace{b+c}{1.0}+d}^{2.0} \overbrace{a+\underbrace{b+c}{1.0}+d}^{2.0}

其它符号

省略号：\(\cdots\) 和 $\ldots$
行内公式: $R^s_r(t_r,t_e)=(t_r-t_e)c$
显示公式: \(R^s_r(t_r,t_e)=(t_r-t_e)c\)

线性模型

\[h(\theta) = \sum_{j = 0} ^n \theta_j x_j\]

均方误差

\[J(\theta) = \frac{1}{2m}\sum_{i = 0} ^m(y^i - h_\theta (x^i))^2\]

批量梯度下降

\[\frac{\partial J(\theta)}{\partial\theta_j}=-\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j\]

参考文献：

https://www.cnblogs.com/jockming/p/14120987.html

https://blog.csdn.net/cui_yonghua/article/details/119382580

https://www.overleaf.com/learn/latex/Chinese

Tutorial
markdown math
This post is licensed under CC BY 4.0 by the author.